Research Interests
Professional curriculum vitae | Electronic publication list | EE Web interview (August 2015)
Environmental Sound Monitoring
Audio Forensics and Gunshot Acoustics
Selected publications, audio forensics:

- R.C. Maher, "Audio forensic analysis procedures for user generated audio recordings," presentation with interactive webinar, National Institute of Justice Forensic Technology Center of Excellence, November, 2022.
- R.C. Maher, Principles of Forensic Audio Analysis, Springer Nature Publishing, 2018.
- R.C. Maher, "Lending an ear in the courtroom: forensic acoustics," Acoustics Today, vol. 11, no. 3, pp. 22-29, 2015.
- R.C. Maher, "Audio forensic examination: authenticity, enhancement, and interpretation," IEEE Signal Processing Magazine, vol. 26, no. 2, pp. 84-94, 2009.
Selected publications, gunshot acoustics:
- R.C. Maher, "Examining tell-tale sounds in forensic gunshot recordings," elib 22634, AES 8th International Conference on Audio Forensics, Denver, CO, June 27-29, 2024.
- S.B. Nesar, B.M. Whitaker, and R.C. Maher, "A geometric approach for generating synthetic gunshot acoustic signals," elib 22631, AES 8th International Conference on Audio Forensics, Denver, CO, June 27-29, 2024.
- S.B. Nesar, B.M. Whitaker, and R.C. Maher, "Machine learning analysis on gunshot recognition," 2024 Intermountain Engineering, Technology and Computing (IETC) Conference, Utah State University, Logan, UT, May 13-14, 2024.
- R.C. Maher, "Close and distant gunshot recordings for audio forensic analysis," Express Paper 122, Proc. 155th Audio Engineering Society Convention, New York, NY, October 27, 2023.
- R.C. Maher, "Interpretation of audio forensic information from the shooting of journalist Shireen Abu Akleh," Express Paper 22, Proc. 153rd Audio Engineering Society Convention, New York, NY, October 20, 2022.
- R.C. Maher, "Forensic interpretation and processing of user generated audio recordings," Preprint 10419, Proc. 149th Audio Engineering Society Convention, New York, NY, Online, October, 2020.
- R.C. Maher and E.R. Hoerr, "Forensic comparison of simultaneous recordings of gunshots at a crime scene," Preprint 10281, Proc. 147th Audio Engineering Society Convention, New York, NY, October, 2019.
- R.C. Maher, "Shot-to-shot variation in gunshot acoustics experiments," elib 20461, Proc. 2019 Audio Engineering Society International Conference on Audio Forensics, Porto, Portugal, June, 2019.
- D.R. Begault, S.D. Beck, and R.C. Maher, "Overview of forensic gunshot analysis techniques," elib 20475, Proc. 2019 Audio Engineering Society International Conference on Audio Forensics, Porto, Portugal, June, 2019.
- R.C. Maher and E.R. Hoerr, "Audio Forensic Gunshot Analysis and Multilateration," Preprint 10100, Proc. 145th Audio Engineering Society Convention, New York, NY, October, 2018.
- R.C. Maher, "Challenges of Audio Forensic Evaluation from Personal Recording Devices," Preprint 9897, Proc. 143rd Audio Engineering Society Convention, New York, NY, October, 2017.
- R.C. Maher and T.K. Routh, "Gunshot acoustics: pistol vs. revolver," Proc. 2017 AES International Conference on Audio Forensics , Arlington, VA, June, 2017; https://doi.org/10.17743/aesconf.2017.978-1-942220-14-5 .
- R.C. Maher and T.K. Routh, "Wideband audio recordings of gunshots: waveforms and repeatability," Preprint 9634, Proc. 141st Audio Engineering Society Convention, Los Angeles, CA, October, 2016.
- T.K. Routh and R.C. Maher, "Recording anechoic gunshot waveforms of several firearms at 500 kilohertz sampling rate," Proc. Mtgs. Acoust. 26, 030001 (2016); http://dx.doi.org/10.1121/2.0000262, May, 2016.
- R.C. Maher, "Gunshot recordings from a criminal incident: who shot first?" J. Acoust. Soc. Am., vol. 139, no. 4, part 2, p. 2024 (abstract), April, 2016. (Lay Language report)
- R.C. Maher and T.K. Routh, "Advancing forensic analysis of gunshot acoustics," Preprint 9471, Proc. 139th Audio Engineering Society Convention, New York, NY, October, 2015.
- R.C. Maher and S.R. Shaw, "Gunshot recordings from digital voice recorders," Proc. Audio Engineering Society 54th Conference, Audio Forensics—Techniques, Technologies, and Practice, London, UK, June 2014.
- R.C. Maher, "A method for enhancement of background sounds in forensic audio recordings," Preprint 8731, Proc. 133rd Audio Engineering Society Convention, San Francisco, CA, October, 2012.
- R.C. Maher and J. Studniarz, “Automatic search and classification of sound sources in long-term surveillance recordings,” Proc. Audio Engineering Society 46th Conference, Audio Forensics—Recording, Recovery, Analysis, and Interpretation, Denver, CO, June 2012.
- R.C. Maher, "Acoustical modeling of gunshots including directional information and reflections," Preprint 8494, Proc. 131st Audio Engineering Society Convention, New York, NY, October, 2011.
- R.C. Maher and S.R. Shaw, "Directional aspects of forensic gunshot recordings," Proc. Audio Engineering Society 39th Conference, Audio Forensics—Practices and Challenges, Hillerød, Denmark, June 2010.
- R.C. Maher, "Acoustical characterization of gunshots," Proc. IEEE SAFE 2007: Workshop on Signal Processing Applications for Public Security and Forensics, Washington, DC, pp. 109-113, April, 2007.
- R.C. Maher, "Modeling and signal processing of acoustic gunshot recordings," Proc. IEEE Signal Processing Society 12th DSP Workshop, Jackson Lake, WY, pp. 257-261, September, 2006.
Journalist reports quoting R.C. Maher:
- New York Times, "Video: How Los Angleles police officers brok protocols and injured protesters" (2025 July 3)
- AP, "US contractors say their colleagues are firing live ammo as Palestinians seek food in Gaza" (2025 July 2)
- CNN, "'Death and hunger’: Videos, expert analysis and witnesses point to Israeli gunfire in Gaza aid site shooting" (2025 June 5)
- CNN, "Exclusive: Intercepted radio chatter and drone footage appear to capture Russian orders to kill surrendering Ukrainian troops" (2025 May 21)
- New York Times, "Six Deadly Minutes: How Israeli Soldiers Killed 15 Rescue Workers in Gaza" (2025 May 2)
- Washington Post, "How Palestinian first responders ended up in a mass grave in Gaza" (2025 April 10)
- BBC, "Israeli army fired as close as 12m in Gaza medics killing, audio suggests" (2025 April 10)
- Sky News, "Israeli troops shot at medics from as close as 12 metres, audio analysis suggests" (2025 April 9)
- Bellingcat, "What Audio Analysis Reveals About Aid Workers Killed in Gaza" (2025 April 9)
- CNN, “Forensic analysis suggests at least 2 weapons were fired at Trump rally” (2024 July 26)
- New York Times, “Speculation swirls about what hit Trump. An analysis suggests it was a bullet” (2024 July 26)
- CBS News, “Trump rally gunman fired 8 shots in under 6 seconds before he was killed, analysis shows” (2024 July 25)
- Washington Post, “Obstructed view may have delayed sniper response at Trump rally” (2024 July 16) (This investigation won the 2025 Pulitzer Prize in Breaking News Reporting )
-
ABC Bozeman, “MSU professor helps with gunfire investigation at former president Trump’s rally” (2024 July 15)
-
New York Times, “Videos show suspect lying motionless on nearby rooftop after shooting” (2024 July 13)
- CNN, "Exclusive: New evidence challenges the Pentagon’s account of a horrific attack as the US withdrew from Afghanistan" (2024 April 24)
- Bellingcat Netherlands, "The Sound of Bullets: The Killing of Colombian Journalist Abelardo Liz" (2023 December 11)
- Washington Post, "A barrage and a midair explosion: What visual evidence shows about the Gaza hospital blast" (2023 October 26).
- U.S. National Institute of Justice, "The Emerging Field of Firearms Audio Forensics" (2023 August 7)
- New York Times, "How Peru Used Lethal Force to Crack Down on Anti-Government Protests" (2023 March 16)
- New York Times, "The Killing of Shireen Abu Akleh: Tracing a Bullet to an Israeli Convoy" (2022 June 20)
- CNN, "'They were shooting directly at the journalists': New evidence suggests Shireen Abu Akleh was killed in targeted attack by Israeli forces" (2022 May 26)
- Bellingcat Netherlands, "Unravelling the Killing of Shireen Abu Akleh" (2022 May 14)
- Daily Beast, "Caught on Tape: National Enquirer Boss’ Secret Plan to Pay R. Kelly $1M" (2019 November).
- St. Louis Public Radio, "Airport Privatization Spokesman 'Very Likely' Called St. Louis On The Air Using a Fake Name," reported by Corinne Ruff (2019 September).
- New York Times, "The English Voice of ISIS Comes Out of the Shadows," reported by Rukmini Callimachi (2019 February).
- Canadian Broadcasting Corporation "Spark" (CBC One radio), "'Audio forensics' helps solve crime through the sound of gunshots," interview by Nora Young (2018 September).
- National Public Radio "Here & Now" (WBUR-Boston), "How Audio Analysis Of Gunshots Helps Solve Crimes," interview by Ms. Robin Young (2017 May).
- BBC News article "Gunfire audio opens new front in crime-fighting," by Richard Gray (2017 May).
- 2017 National Institute of Justice R&D Symposium, "Just Science interviews Dr. Rob Maher," podcast interview by Dr. John Morgan (2017 February).
- Forbes.com Tech "Acoustic Gunshot Analysis Could Help Solve Crimes" by Jennifer Hicks (2016 June)
- Science News "Sounds from gunshots may help solve crimes," by Dr. Meghan Rosen (2016 June)
- ExpertPages Blog "Lighting and Audio Experts Testify in Trial of Cleveland Police Officer Accused of Manslaughter," by Colin Holloway (April 2015)
- Bozeman Daily Chronicle feature article on audio forensics by Ms. Whitney Bermes (2013 April)
- (link to corresponding photo gallery and newspaper page image pdf)
- MSU News Service article on audio forensics research by Mr. Sepp Jannotta (2013 March)
- "The American Private Investigator" podcast (.mp3), audio forensics interview by Mr. Paul Jaeb (2013 February).
- Forensic Magazine interview article on gunshot acoustical analysis by Mr. Douglas Page (2012 October)
- Electronic Design interview article on gunshot analysis by Mr. John Edwards (2007 September)
- "Focus on Technology" Radio interview (.mp3) by Ms. Ann Thompson, WVXU Cincinnati (2007 March)
- Scienceline article on gunshot analysis by Mr. Jeremy Hsu (2007 January); reprinted in LiveScience (2007 March)
- MSU News Service article on audio research by Mr. Tracy Ellig (2006 November); reprinted in ScienceDaily , Physorg.com, EurakAlert, Innovations Report,Medical News Today, and Environmental Protection Online
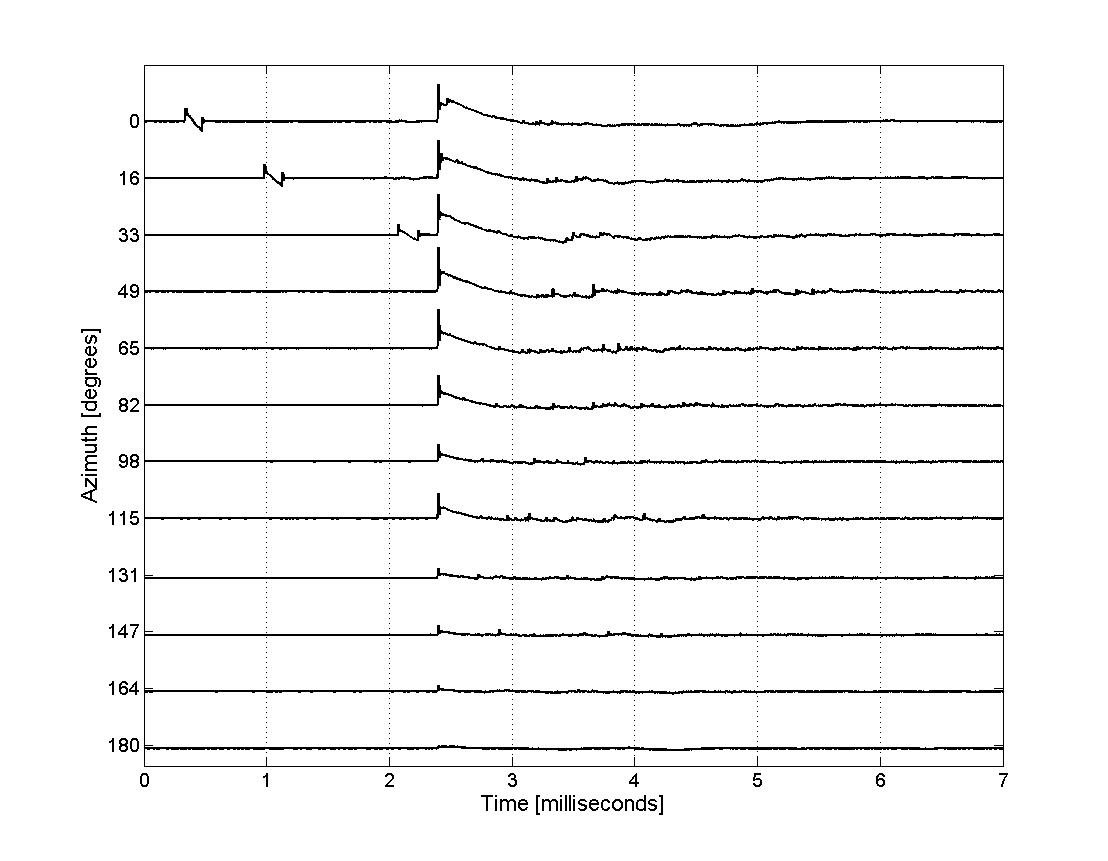
- Example gunshot observation raw data.
Ecological Sound Monitoring and Interpretation

- Baseline soundscape analysis project for Grant-Kohrs Ranch National Historic Site (2009-2010)
- R.C. Maher, "Acoustics of national parks and historic sites: the 8,760 hour MP3 file," Preprint 7893, Proc. 127th Audio Engineering Society Convention, New York, NY, October, 2009.
- Z. Chen and R.C. Maher, "Semi-automatic classification of bird vocalizations using spectral peak tracks," J. Acoust. Soc. Am., vol. 120, no. 5, pp. 2974-2984, November, 2006.
- S.M. Pascarelle, B. Stewart, T.A. Kelly, A. Smith, and R.C. Maher, "An Acoustic / Radar System for Automated Detection, Localization, and Classification of Birds in the Vicinity of Airfields," 8th Joint Annual Meeting of Bird Strike Committee USA/Canada, St. Louis, MO, August, 2006.
- R.C. Maher, J. Gregoire, and Z. Chen, "Acoustical monitoring research for national parks and wilderness areas," Preprint 6609, Proc. 119th Audio Engineering Society Convention, New York, NY, October, 2005.
- G. Sanchez, R.C. Maher, and S. Gage, "Ecological and environmental acoustic remote sensor (EcoEARS) application for long-term monitoring and assessment of wildlife," U.S. Department of Defense Threatened, Endangered and at-Risk Species Research Symposium and Workshop, Baltimore, MD, June, 2005
- White paper on National Park sound inventories (2004 January)
The project involves two phases. In the first phase a set of algorithms are developed to identify and classify a variety of acoustical sound sources, such as jet aircraft, propeller aircraft, helicopters, snowmobiles, automobiles, and bioacoustic sounds, obtained with a high quality digital recording. The identification and classification are carried out using a fast time-frequency decomposition of the input signal followed by a maximum likelihood matching procedure.
In the second phase a rugged and self-contained monitoring platform is designed and constructed. The platform contains a digital signal processor (DSP), a microphone and data acquisition subsystem, a memory subsystem, and a solar power supply. The platform is intended to be deployed in a remote location for perhaps several weeks at a time, while continuously monitoring and classifying the acoustical environment. The data is then downloaded to a computer for further analysis and the preparation of an acoustical profile.
Automatic Decomposition and Classification of Sounds in Audio Recordings
It is very common in many applications to have an audio recording that contains a desired signal source (the target) and one or more competing sources (the jammers). In this situation it is necessary to enhance the desired source and attenuate the competing sources. For example, the desired source may be a person talking on a cell phone, while the competing sources may be other talkers, ambient wind and traffic noise, or electromagnetic interference in the communications channel.
- R.C. Maher, "A method for enhancement of background sounds in forensic audio recordings," Preprint 8731, Proc. 133rd Audio Engineering Society Convention, San Francisco, CA, October, 2012.
- R.C. Maher and J. Studniarz, “Automatic search and classification of sound sources in long-term surveillance recordings,” Proc. Audio Engineering Society 46th Conference, Audio Forensics—Recording, Recovery, Analysis, and Interpretation, Denver, CO, June 2012.
- B.J. Gregoire and R.C. Maher, "Map seeking circuits: a novel method of detecting auditory events using iterative template mapping," Proc. IEEE Signal Processing Society 12th DSP Workshop, Jackson Lake, WY, pp. 511-515, September, 2006.
- R.C. Maher, "Audio enhancement using nonlinear time-frequency filtering," Proc. Audio Engineering Society 26th Conference, Audio Forensics in the Digital Age, Denver, CO, July 2005.
- B.J. Gregoire and R.C. Maher, "Harmonic Envelope Detection and Amplitude Estimation Using Map Seeking Circuits," Proc. IEEE International Conference on Electro Information Technology (EIT2005), Lincoln, NE, May, 2005.
- J. Gregoire and R.C. Maher, "Map seeking circuits for audio pattern recognition," Music Information Processing Workshop, Whistler, British Columbia, Canada, December, 2004.
Acoustical Modeling of Environments and Architectural Spaces

As would be expected, much of the work on architectural auralization is achieved using digital computer simulations. Like computer graphics, many auralization systems use a ray tracing model or an image model in which the computer program computes a series of reflections from a particular sound source location to the various surfaces in the room and then to a particular listener location. If the room is of a simple geometry, such as a rectangular floor plan, the computation of the various sound ray reflections can be accomplished in a straightforward manner. The interaction of sound waves with objects and surfaces encountered in a room has been treated using a variety of modeling techniques. The current scheme used in many acoustical modeling systems consists of an early reflection model coupled with a late reverberation model.
- D. Reed and R.C. Maher, "An investigation of early reflection’s effect on front-back localization in spatial audio," Preprint 7884, Proc. 127th Audio Engineering Society Convention, New York, NY, October, 2009.
- Z. Chen and R.C. Maher, "Analytical expression for impulse response between two nodes in 2-D rectangular digital waveguide mesh," IEEE Signal Processing Letters, vol. 15, pp. 221-224, 2008.
- Z. Chen and R.C. Maher, "Addressing the Discrepancy Between Measured and Modeled Impulse Responses for Small Rooms," Preprint 7239, Proc. 123rd Audio Engineering Society Convention, New York, NY, October, 2007.
- Z. Chen and R.C. Maher, "Modeling room impulse response by incorporating speaker polar response into image source method," J. Acoust. Soc. Am. , vol. 121, no. 5, part 2, p. 3174 (abstract), 2007.
The simple image model of the early reflections is known to be inadequate to describe the diffuse reflections that occur when sound waves hit typical surfaces, particularly for frequencies above 200 Hz. The reason that these compromises are usually used is that the computation required to do higher-order modeling has been too high for practical implementation in real-time systems. Even with fast computers, the complexity of the image model is of the order nr, where n is the number of surfaces and ris the number of reflections calculated, and this makes simulating anything but the simplest of listening spaces intractable.
This research project involves two approaches in an attempt to improve the accuracy of the acoustical simulation while avoiding the excessive computational complexity. The first approach is to pre-calculate an estimate of the acoustical transfer function from the source to the vicinity of the listener, and then to convolve this pre-calculated response with the desired sound source signal. The second approach is less “brute force,” and will require research to discover the most efficient means of representation. Rather than treating the acoustical wave propagation using a ray model in which the angle of incidence equals the angle of reflection at each surface, a wavefront model is proposed to account for the diffuse sound energy that reflects in directions other than the specular angle.
Pitch Transitions in Vocal Vibrato

A common characteristic of singing by trained vocalists is vibrato. Typical vocal vibrato is a roughly sinusoidal variation in frequency of +/- 2%, with a repetition rate of about 5 Hz. Vibrato is caused by a periodic change in the tension of the vocal folds and glottis. The resulting frequency sweep of the fundamental and harmonics tends to enhance the richness of the singer’s voice as the spectral partials interact with the resonances of the throat, mouth, and sinuses. In particular, the FM of the glottal excitation can induce AM effects for partials that coincide with peaks, troughs, or shoulders of the fixed vocal tract resonances. In addition to the physical acoustics of vibrato, there are a variety of common singing practices that are learned indirectly during vocal instruction, but are usually not described explicitly. One of these behaviors is how vibrato is handled at the transition from one sung pitch to another during legato (no break in the sound) singing. In this investigation a set of recordings of trained singers performing simple legato arpeggios has been obtained so that an analysis can be performed on the instantaneous fundamental frequency before, during, and after the pitch transition. This work is intended to provide both a phenomenological description and a set of parameters suitable for realistic vocal synthesis.
R.C. Maher, "Control of synthesized vibrato during portamento musical pitch transitions," J. Audio Eng. Soc., vol. 56, no. 1/2, pp. 18-27, 2008.
Evaluation of Numerical Precision in the MDCT and Other Transforms
The use of fast numerical algorithms in waveform and image coding often involves the modified discrete cosine transform (MDCT) or similar procedures. However, the effects of round-off errors and coefficient quantization are not well understood in the MDCT, and so in practical systems it is difficult to choose the required number of bits to represent the coefficients and to store the intermediate results. In the proposed project a theoretical analysis of the numerical precision issues for the MDCT will be conducted. The results will help guide future designers in the optimal implementation of signal coding schemes.
Efficient Architectures for Audio Digital Signal Processing
Modern audio signal processing systems are noted for concurrent processing requirements: simultaneous mixing, music synthesis, sample rate conversion, audio effects, and decoding of compressed audio. It has been common to design either a special-purpose hardware processor for each function or to utilize software on a general-purpose processor in order to accomplish the required concurrency. However, the resulting system is typically unsatisfactory either due to the cost of designing and fabricating the special circuitry, or due to the reduced performance of a totally software-based implementation. This research will develop a scalable architecture in which the available hardware resources are assigned specific processing tasks according to the current user requirements. By assigning the resources dynamically and monitoring the actual system loading, the architecture provides a more efficient and economical system than is obtained by conventional methods.
- R.C. Maher and J. Barish, "Scalable Audio Processing on a Heterogeneous Processor Array," U.S. Patent Number 6,301,603, October 9, 2001.
Lossless Compression of Audio Signals
Audio recordings generally do not allow significant lossless data compression using conventional techniques such as Huffman, Arithmetic Coding, or Lempel-Ziv. A 50% compressed size would be considered useful, but typical compressed audio files are still 70-90% of the original file size. Lossy compression, and in particular perceptual coding, can achieve compressed files that are as little as 10% of the original file size, but the original data is not recovered exactly. If the lossy compression is perceptually lossless, the decoded data cannot be distinguished by a human listener and it might seem that the problem is solved. However, there are many applications in which lossless compression is essential or highly desirable, such as archiving data that will subsequently be mixed or processed, preparation of temporary or permanent backup copies, and transmission of data through channels that will require a series of compression/decompression steps (tandeming) in which the distortion due to lossy compression would build up. In this investigation a signal segmentation process is employed to separate the audio data into segments with specific signal properties, followed by a dynamic codebook adaptive coder to represent each segment. The process is asymmetrical: the encoder complexity is generally much greater than the decoder complexity.
- R.C. Maher, "Lossless Audio Coding," book chapter, Lossless Compression Handbook, K. Sayood, ed., San Diego: Academic Press, 2003.
- R.C. Maher, "A method for enhancement of background sounds in forensic audio recordings," Preprint 8731, Proc. 133rd Audio Engineering Society Convention, San Francisco, CA, October, 2012.
- R.C. Maher and J. Studniarz, “Automatic search and classification of sound sources in long-term surveillance recordings,” Proc. Audio Engineering Society 46th Conference, Audio Forensics—Recording, Recovery, Analysis, and Interpretation, Denver, CO, June 2012.
- R.C. Maher, "Acoustical modeling of gunshots including directional information and reflections," Preprint 8494, Proc. 131st Audio Engineering Society Convention, New York, NY, October, 2011.
- R.C. Maher and S.R. Shaw, "Directional aspects of forensic gunshot recordings," Proc. Audio Engineering Society 39th Conference, Audio Forensics—Practices and Challenges, Hillerød, Denmark, June 2010.
- Electronic Design interview article on gunshot analysis by Mr. John Edwards (2007 September)
- R.C. Maher, "Acoustical characterization of gunshots," Proc. IEEE SAFE 2007: Workshop on Signal Processing Applications for Public Security and Forensics, Washington, DC, pp. 109-113, April, 2007.
